Opracował:
Prof. Roman Słowiński,
9 lutego 2008r.
Instytut Informatyki
Politechniki Poznańskiej

1. Dane wejściowe

Jednostki ocenione są za pomocą następujących czterech wskaźników liczbowych, zwanych kryteriami głównymi:

· g₁ – kryterium pozycji akademickiej jednostki,

· g₂ – kryterium pozycji naukowej kadry,

· g₃ – kryterium infrastruktury jednostki,

· g₄ – kryterium studiów i studentów.

Kryteria te przyjmują wartości liczbowe w różnym zakresie wartości. Agregują one wartości podkryteriów szczegółowych, zwanych wskaźnikami, zdefiniowanych przez zespół ds. oceny.

Im większa wartość na danym kryterium, tym ocena jednostki jest lepsza.

Nie zakłada się prostej kompensacji między kryteriami, gdyż nie da się jednoznacznie ustalić współczynników wymiany między poszczególnymi kryteriami głównymi, tzn. jaki wzrost oceny na kryterium g_i kompensuje spadek oceny na kryterium g_j o jednostkę, i, j=1,…,4, i¹j, w dowolnym zakresie wartości obu kryteriów.

2. Wybór metody

Konstrukcja listy rankingowej jednostek ocenionych za pomocą n kryteriów należy do kategorii problemów wielokryterialnego porządkowania obiektów.

Z powodu odrzucenia prostej kompensacji między kryteriami, metoda agregacji ocen wielokryterialnych za pomocą tzw. „sumy ważonej” ocen na poszczególnych kryteriach nie będzie stosowana.

Porządek jednostek w zbiorze zależy od relacji pomiędzy parami jednostek w tym zbiorze.

Jedyną obiektywną relacją porządkującą zbiór jednostek jest relacja dominacji D.

Jednostka a dominuje jednostkę b (zapis: aDb) wtedy i tylko wtedy, gdy a jest nie gorsza od b na wszystkich n kryteriach, w tym przynajmniej na jednym kryterium jest lepsza, co zapisujemy: aDb Û g_i(a) ³ g_i(b), i=1,…,n, $jÎ{1,…,n}: g_j(a) > g_j(b).

Relacja dominacji D jest preporządkiem częściowym (zwrotna i przechodnia), czyli w ogólności nie porządkuje wszystkich jednostek ze zbioru. Innymi słowy, część jednostek jest nieporównywalna za pomocą relacji dominacji D.

Ponieważ warunek prawdziwości relacji dominacji jest w praktyce trudny do spełnienia, zwykle duża część zbioru jednostek pozostanie nieporównywalna za pomocą tej relacji.

Aby zwiększyć porównywalność jednostek w stosunku do relacji dominacji należy zastąpić ją relacją o słabszych wymaganiach, zgodnych z preferencjami zespołu oceniającego. Nazwijmy tę relację relacją przewyższania S.

Relacja przewyższania S ma być zwrotna lecz nie musi być przechodnia. Jeśli jednostka a przewyższa jednostkę b (zapis: aSb), to mówimy, że „a jest co najmniej tak dobra jak b”.

Proponowaną definicję relacji przewyższania podamy w punkcie 3.

Przyjmijmy, że na podstawie znajomości ocen jednostek na n kryteriach głównych, wyznaczono relację przewyższania S dla każdej pary (a,b) jednostek.

Relację S w zbiorze jednostek można przedstawić w postaci grafu skierowanego, w którym wierzchołki odpowiadają jednostkom, a łuki relacjom przewyższania, w ten sposób, że łuk wychodzi z wierzchołka a do wierzchołka b wtedy i tylko wtedy, gdy a przewyższa b (aSb).

Przykładowy graf relacji przewyższania pokazano na Rysunku 1.

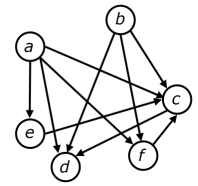
Rysunek 1. Przykładowy graf relacji przewyższania

W celu skonstruowania listy rankingowej jednostek na podstawie grafu relacji przewyższania proponuje się zastosowanie metody „rangowania na podstawie przepływu netto” (ang. Net Flow Score).

Na każdym łuku (a,b) występuje przepływ równy stopniowi prawdziwości relacji przewyższania S. Dla relacji S zero-jedynkowej, przepływ na łuku wynosi 1.

Pozycja jednostki a w rankingu wynika z bilansu przepływu na łukach wychodzących i wchodzących do wierzchołka a. O bilansie tym mówi wynik „netto”, oznaczony przez NSF(a):

NFS(a) = (suma przepływów wychodzących z a) – (suma przepływów wchodzących do a),

czyli,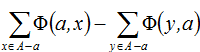

W powyższym przykładzie, przyjmując, że przepływ na każdym łuku wynosi 1, otrzymamy wartości NSF przedstawione w Tabeli 1 i ranking przedstawiony na Rysunku 2.

Tabela 1. Wartości NFS

3. Proponowana definicja relacji przewyższania S

Istnieją tu różne możliwości, z których w naszej sytuacji najlepsza wydaje się definicja „większościowa z możliwością veta od kryteriów niezgodnych”. Konstrukcja relacji przewyższania S ma wtedy charakter niekompensacyjny, a S jest relacją zwrotną i nieprzechodnią.

Niech D_i oznacza wartość odchylenia standardowego w zbiorze ocen jednostek na kryterium g_i, i=1,…,n.

Przy porównywaniu pary jednostek (a,b) na każdym pojedynczym kryterium g_i, i=1,…,n, przyjmiemy, że:

· jednostki a i b są nierozróżnialne na kryterium g_i, gdy -0.2D_i £ g_i(a) - g_i(b) £ 0.2D_i,

· jednostka a jest preferowana nad jednostkę b na kryterium g_i,
gdy g_i(a) - g_i(b) > 0.2D_i.

Definicja:

Jednostka a przewyższa jednostkę b (zapis: aSb), wtedy i tylko wtedy, gdy a jest nierozróżnialna lub preferowana nad b na większości kryteriów, a ponadto, na pozostałych kryteriach, a jest nie gorsza od b o więcej niż dwie wartości odchylenia standardowego:

W grafie relacji przewyższania przepływ od wierzchołka a do b przyjmuje wartość: